В этой статье я пошагово смоделирую упругий элемент пневмогидравлической подвески в приложении Simulink с использованием стандартных библиотек SimHydraulics.
1 Введение
Пневмогидравлическая подвеска (ПГР) по сравнению со стальными упругими элементами имеет следующие преимущества:
- высокую удельную энергоемкость (отношение полной работы рессоры к объему рабочего тела, т.е. конечному объему газа для ПГР или объему металла для металлических упругих элементов), которая примерно в 30-40 раз выше, чем у листовых рессор, и в 10-15 раз выше, чем у пружин и торсионов, в результате чего снижается масса и габариты подвески;
- сочетание в одном узле упругих и демпфирующих устройств, в результате чего отпадает необходимость применения гидравлического амортизатора как отдельного узла;
- нелинейность упругой характеристики, что способствует повышению плавности хода, снижению вероятности пробоя и возможности существенного увеличения грузоподъемности при ограниченных ходах подвески.
Применение ПГР актуально в КМ, где традиционные подвески с металлическими упругими элементами и гидравлическими амортизаторами не подходят из-за низкой удельной энергоемкости и сложности получения оптимальных упругодемпфирующих характеристик для разнообразных условий эксплуатации, особенно по разбитым дорогам.
Однако известные конструкции ПГР не решают всего комплекса требований, предъявляемых к КМ, и имеют некоторые недостатки, например: сравнительно низкая стабильность их характеристик вследствие внутренних и внешних утечек жидкости и газа, низкой долговечности уплотнительных узлов и температурной чувствительности.
Ниже представлена модель пневмогидравлического элемента, состоящего из цилиндра, в котором установлены поршень и шток, дополнительного цилиндра с плавающим поршнем, образующие гидравлическую и пневматическую полости гидроаккумулятора ПГР. Цилиндры установлены в корпусе, в котором имеется канал, соединяющий их через клапан, выполненный в виде саморегулируемого по частоте и амплитуде колебаний демпфирующего узла.
1.1 Имитационное моделирование
Для оценки параметров пневмогидравлической подвески используется метод имитационного моделирования. Этот способ дает возможность экспериментировать с системой в тех случаях, когда делать это на реальном объекте практически невозможно или нецелесообразно.
Имитационное моделирование есть процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить (в рамках ограничений, накладываемых некоторым критерием или совокупностью критериев) различные стратегии, обеспечивающие функционирование данной системы. Под моделью реальной системы мы понимаем представление группы объектов или идей в некоторой форме, отличной от их реального воплощения [1].
Имитационное моделирование является экспериментальной и прикладной методологией, имеющей целью:
- описать поведение систем;
- построить теории и гипотезы, которые могут объяснить наблюдаемое поведение;
- использовать эти теории для предсказания будущего поведения системы, т.е. тех воздействий, которые могут быть вызваны изменениями в системе или изменениями способов ее функционирования.
В отличие от большинства технических методов, которые могут быть классифицированы в соответствии с научными дисциплинами, в которые они уходят своими корнями (например, с физикой или химией), имитационное моделирование применимо в любой отрасли науки.
Все имитационные модели представляют собой модели типа так называемого черного ящика. Это означает, что они обеспечивают выдачу выходного сигнала системы, если на ее взаимодействующие подсистемы поступает входной сигнал.
В работе применяется математическое имитационное моделирование. Работа подвески моделируется с помощью системы дифференциальных уравнений, которая затем решается численным методом.
1.2 Начальные параметры системы
Для создания имитационной модели ПГР необходимо знать некоторые исходные параметры этой подвески. Для этого был проведен расчет оценки плавности хода по раздельно-частотному методу в программе MathCad. Этот метод подразумевает, что заданный частотный диапазон разбивается на поддиапазоны, в каждом из которых рассчитываются показатели вибрационной нагрузки. Согласно [3] в предварительном расчете используется выбранный постоянный коэффициент упругости подвески , что снижает точность вычислений. Используя имитационную модель, можно получить более точное значение коэффициента упругости без использования реальных испытаний подвески. Ниже представлена линейная система с постоянным коэффициентом упругости:
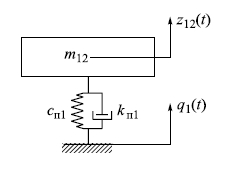
Исходные параметры системы:
- Cп = 2,1*105 Н/м – коэффициент упругости подвески;
- kaот = 1,604104 Нс/м - коэффициент сопротивления на ходе отбоя;
- kaсж = 2,674103 Нс/м - коэффициент сопротивления на ходе сжатия;
- mнагрПО = 7200 кг - масса нагруженной КМ, приходящейся на переднюю ось;
- Vстат = 0,000679 м3 - объем газа в цилиндре при статическом положении;
- Sпш = 0,00447 м2 – площадь поршня;
- pстат = 9 МПа – статическое давление газа;
- pатм = 0,1 МПа – атмосферное давление;
- n = 1,2 – показатель политропы.
2 Построение имитационной модели упругого элемента пневмогидравлической подвески
При построении модели был принят ряд допущений:
- отсутствуют утечки жидкости, внутренние и внешние;
- не принимается во внимание инерционность и сжимаемость жидкости;
- газ считается идеальным;
- процессы в газовой полости являются политропными;
- отсутствует трение между поршнями и цилиндрами.
Особенностью моделирования с помощью SimHydraulics является использование стандартных блоков, которые отражают физические свойства различных элементов гидросистемы. При этом связь этих блоков аналогична соединению реальных объектов трубопроводом – приложение автоматически составляет уравнения связи.
На вход модели подается сигнал, характеризующий скорость перемещения поршня в основном цилиндре. Скорость принимаем постоянной и равной 0,08 м/с. Скорость достаточно мала, чтобы по возможности максимально уменьшить искажение нагрузочной характеристики упругого элемента из-за наличия потерь на демпфирование.
Используемые компоненты:
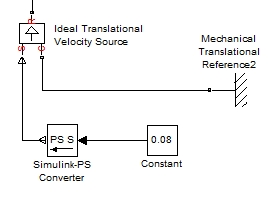
На входной порт S блока “Ideal translational velocity source” поступает физический сигнал, задающий нужную скорость. Порт R является выходным и соединен с поршнем цилиндра. Порт C связан с системой отсчета физического сигнала.
Система отсчета является жесткой и неподвижной, что задается блоком “Mechanical translational elements”.
Скорость является постоянной и устанавливается блоком “Constant”.
Блок “Simulink-PS Converter” позволяет преобразовать стандартный сигнал Simulink в физический.
В итоге получаем следующую систему:
Следующий набор блоков:
Цилиндр с установленным в нём штоком и поршнем моделируется блоком “Single-Acting Hydraulic Cylinder”. Порт R является механическим и соединяется с ранее описанной системой. Порт C связан с системой координат, являющейся жесткой и неподвижной. Порт A является выходным и соединяется с газовым аккумулятором, с помощью которого моделируется дополнительный цилиндр ПГР, имеющий газовую и гидравлическую полости, разделенные между собой подвижным поршнем.
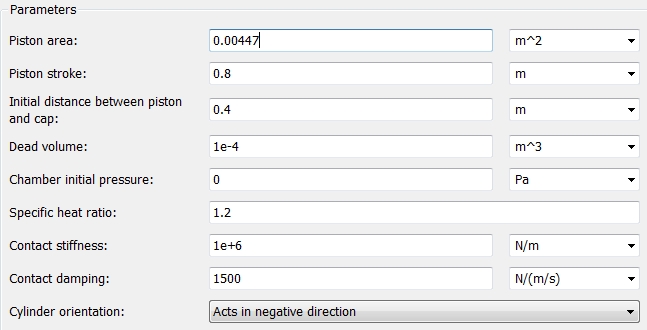
Для этого блока необходимо задать настройки, связанные с площадью поршня (Piston Area), его ходом (Piston stroke), начальным положением поршня относительно цилиндра (Initial distance between piston and cap), объемом жидкости при полностью выдвинутом штоке (Dead volume), начальным давлением в гидравлической полости цилиндра (Chamber initial pressure), показателем политропы (Specific heat ratio), жесткостью (Contact stiffness) и коэффициентом демпфирования (Contact damping) ограничителя хода. Часть значений оставляем предложенными программой по умолчанию:
Между газовым аккумулятором и цилиндром устанавливаем датчик давления “Hydraulic Pressure Sensor”. Порт A входной и связан с цилиндром, а порт B – выходной и соединен с газовой полостью. Порт P позволяет снять физический сигнал и передать его для дальнейшей обработки.
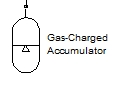
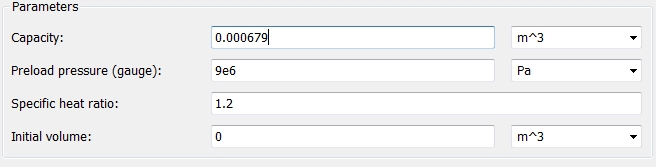
Блок “Gas-charged accumulator” представляет собой гидравлическую и газовую полости, разделенные плавающим поршнем. Блок имеет только один входной порт. В его настройках указываем объем газа (Capacity), статическое давление (Preload pressure) и другие параметры:
Для построения нагрузочной характеристики необходимо снимать два параметра: силу и перемещение поршня.
Для получения действующей величины силы используем значение давления, полученное ранее с помощью блока “Hydraulic Pressure Sensor”, и умножаем его на площадь поршня. Для этого потребуется блок “Gain”.
Блок имеет входной и выходной порты. Устанавливаем величину площади поршня в настройках.
Чтобы получить величину перемещения поршня устанавливаем блок “Ideal Translational Motion Sensor”. Он имеет 4 порта: один механический R, другой C связан с системой координат, 2 остальных V и P позволяют определить скорость и перемещения поршня.
Блок “Scope” отображает зависимость величины, поступающей на входной порт, от времени. Он требуется для построения графических зависимостей перемещения поршня, давления и силы от времени.
С помощью блока “XY Graph” построим нагрузочную характеристику собранной модели.
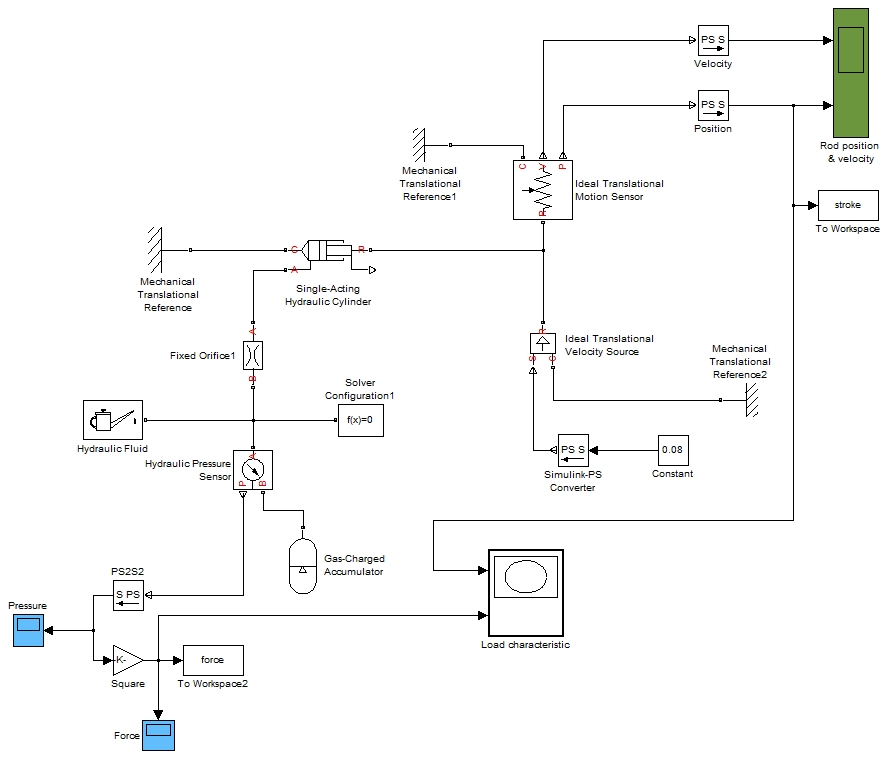
Соединив описанные блоки, получим имитационную модель пневмогидравлической подвески:
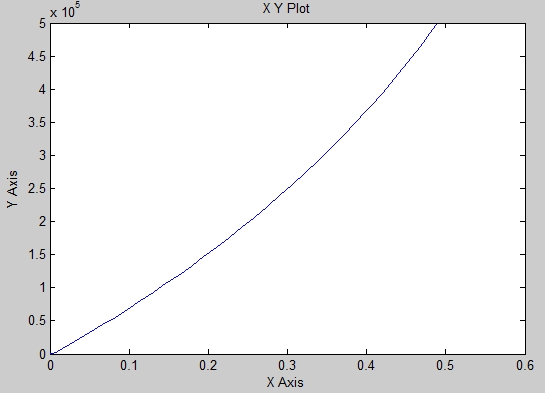
Запускаем полученную модель и получаем на выходе следующий результат:
Таким образом, была получена нагрузочная характеристика упругого элемента пневмогидравлической подвески с использованием имитационного моделирования.
3 Имитационная модель движения автомобиля по дороге с гармоническим профилем
Для того чтобы в первом приближении исследовать неточности расчёта плавности хода, которые получаются при допущении о постоянстве жёсткости подвески, используется имитационная модель движения автомобиля по дороге с гармоническим профилем.
Ранее была получена нагрузочная характеристика ПГР с помощью имитационного моделирования. Зная текущее положение поршня и создаваемое усилие, можно определить величину коэффициента упругости в данный момент времени.
Запишем уравнение движения для линейной системы:

Используя MatLab, получим зависимости ускорения z'', скорости z' и перемещения z подрессоренной массы КМ от времени. В качестве коэффициента упругости сначала используем постоянное значение, затем подставляем значения, полученные с помощью имитационной модели.
На ходе отбоя и сжатия подвеска имеет разные коэффициенты демпфирования, поэтому используем блок “Switch”, позволяющий изменять нужное значение в зависимости от заданного условия.
В качестве кинематического воздействия на подвеску используем блок “Sine wave”, позволяющий задать синусоидальный профиль.
Для суммирования или вычитания значений используется блок “Sum”, имеющий неограниченное число входов и один выход.
Блок “Derivative” предназначен для получения производной входного сигнала по времени.
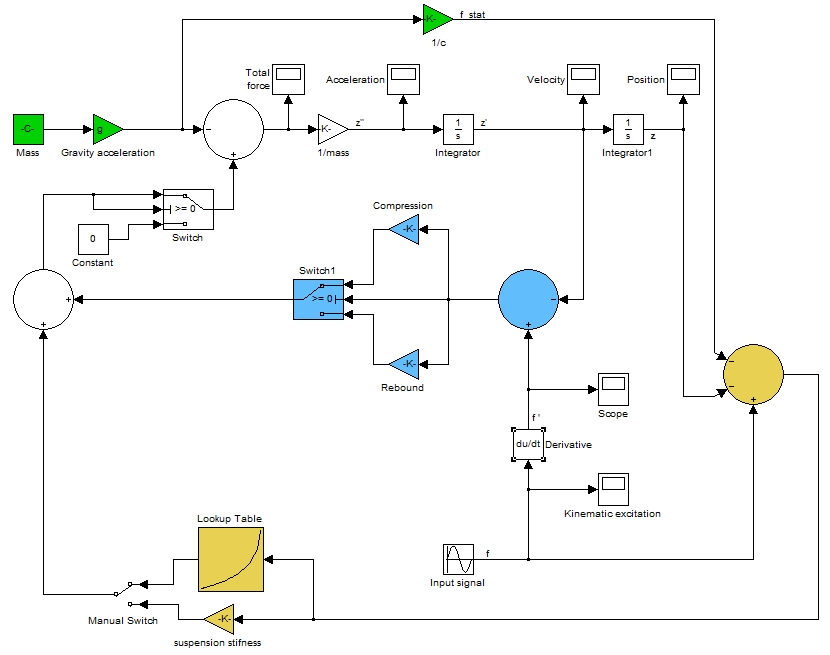
Используя описанные ранее блоки, была получена следующая математическая модель:
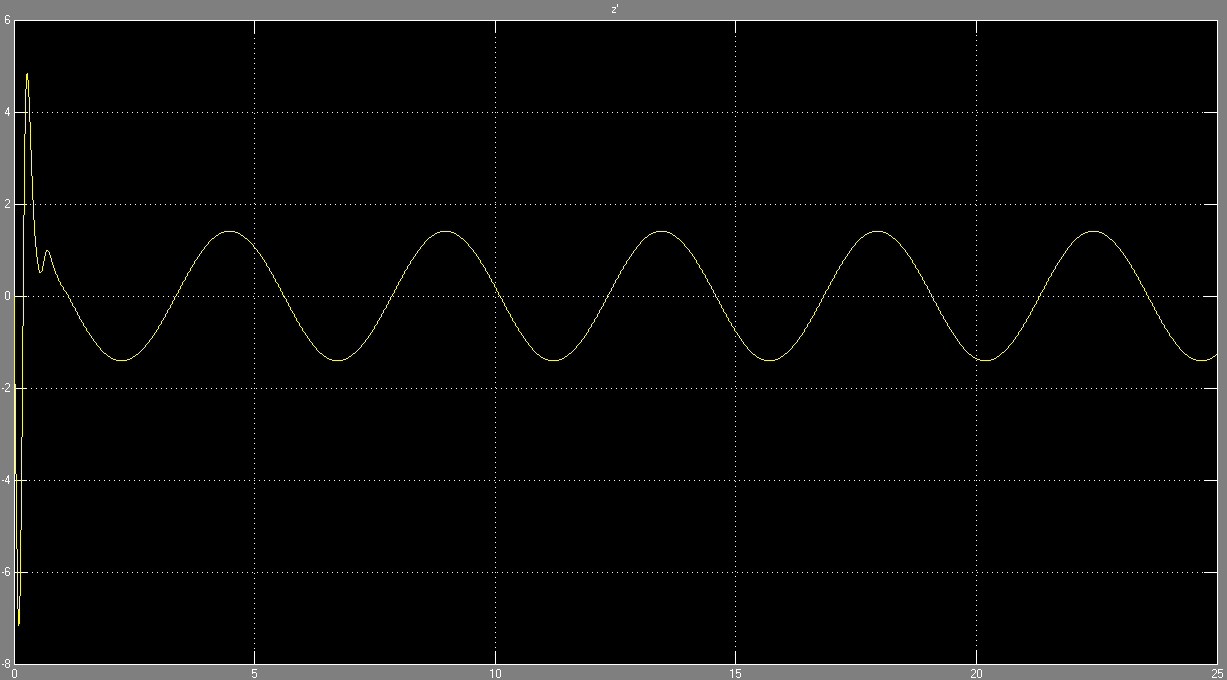
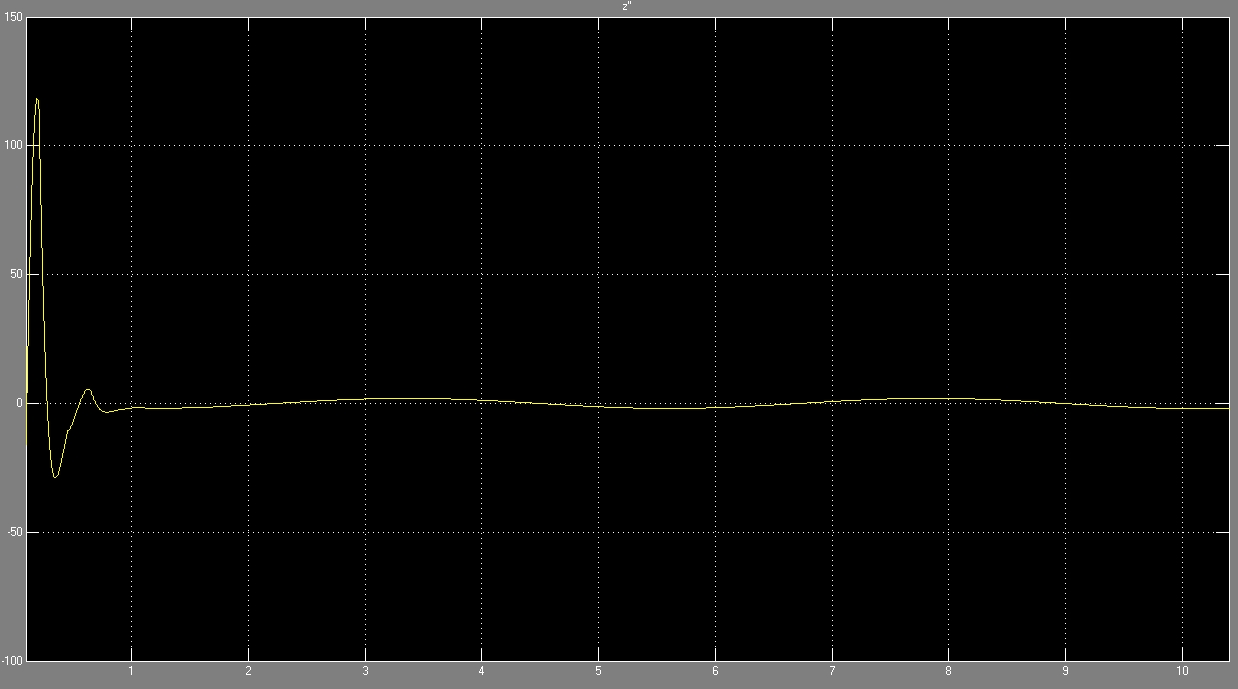
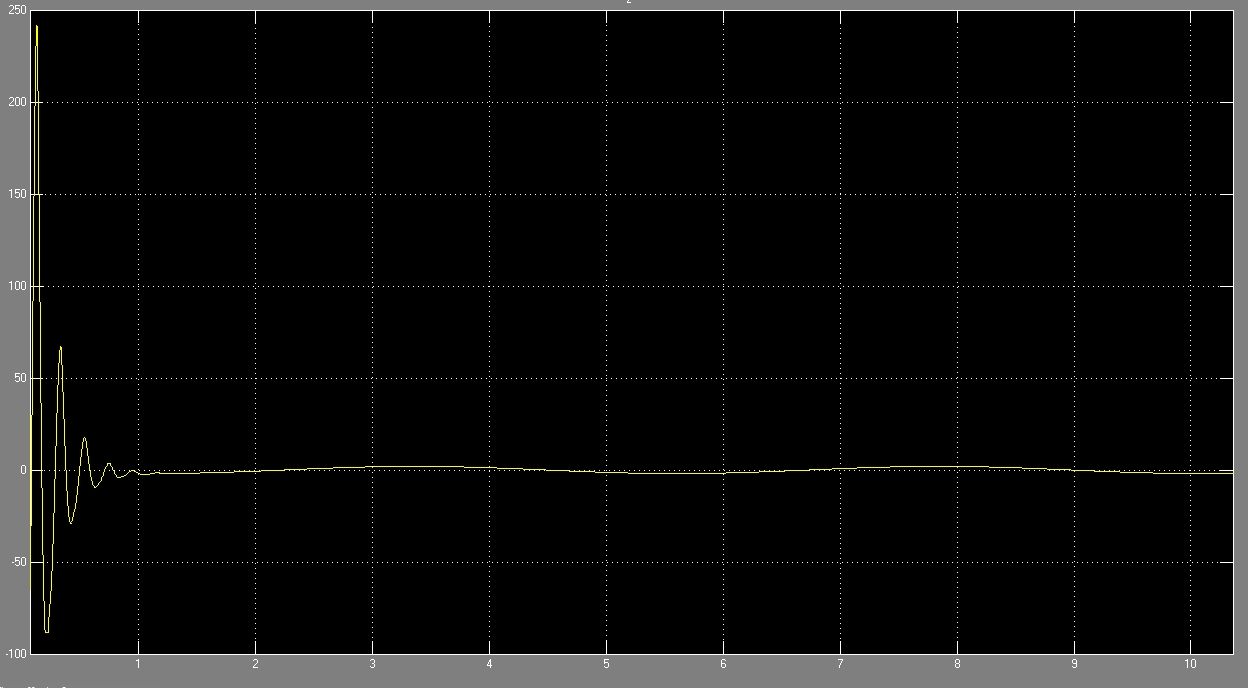
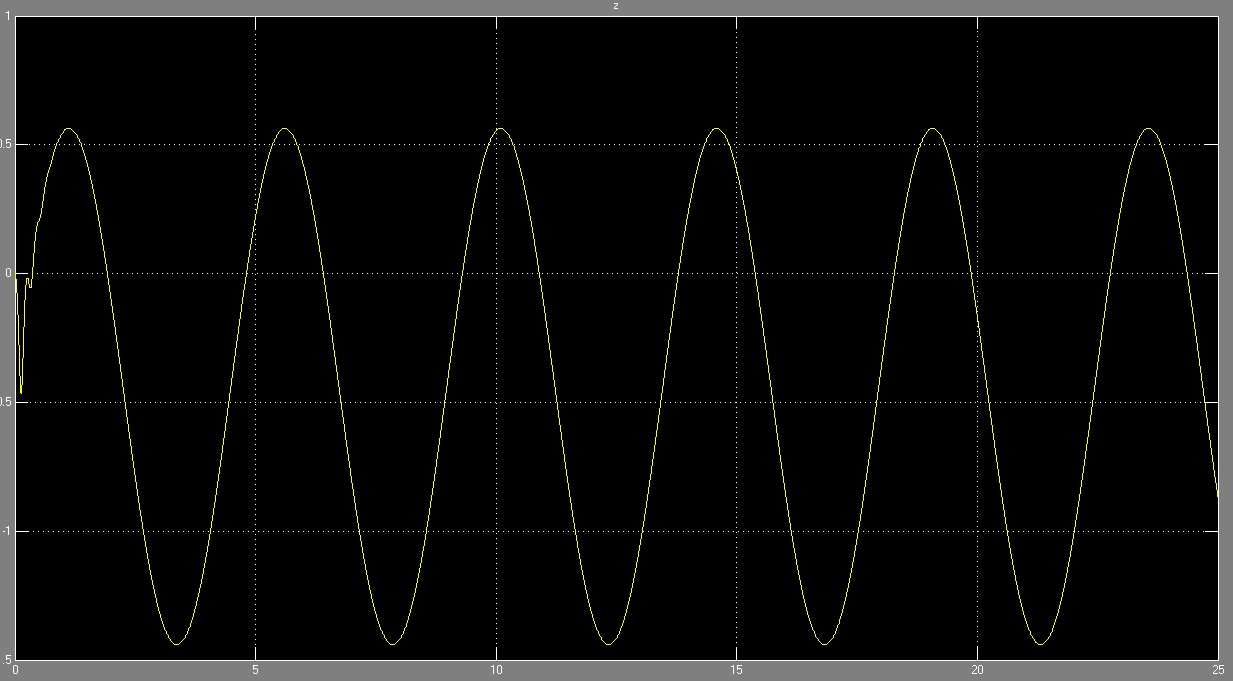
Полученные графические зависимости при постоянном коэффициенте упругости:
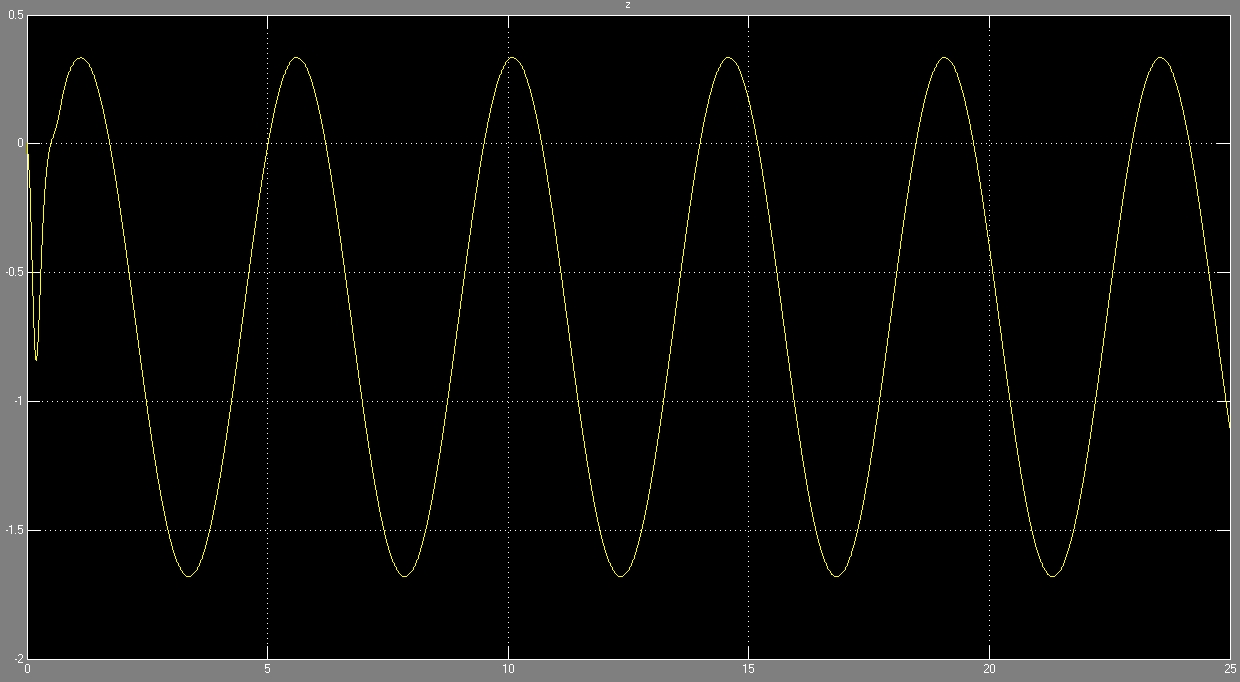
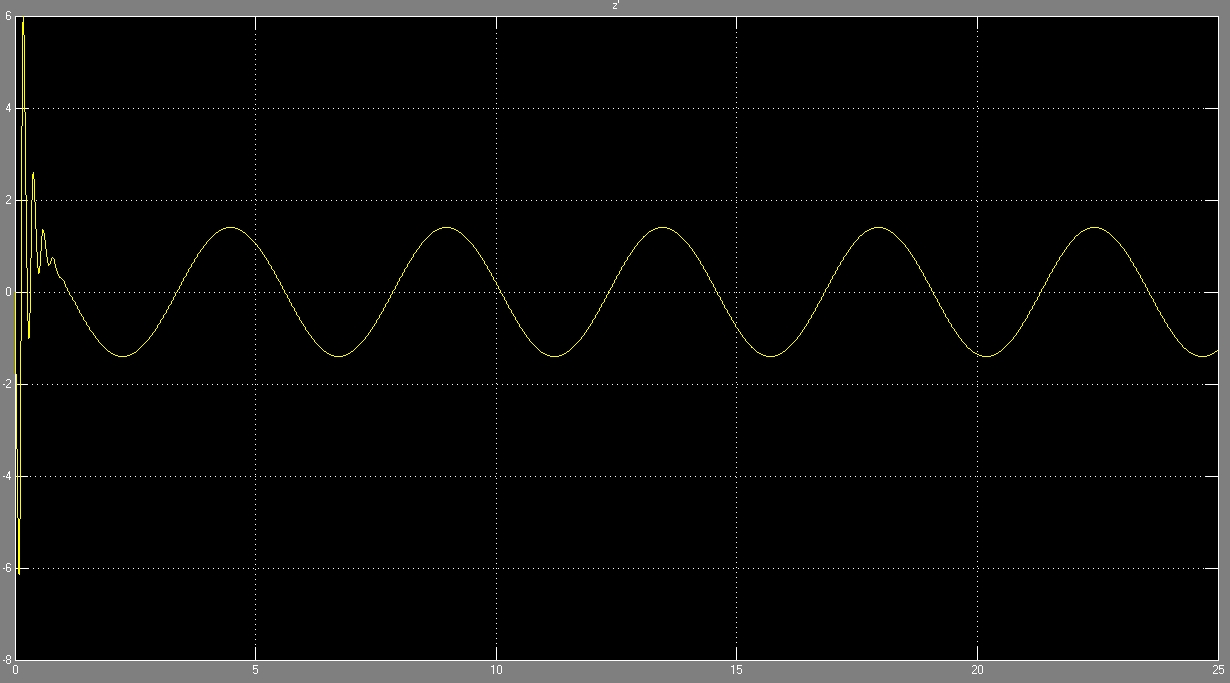
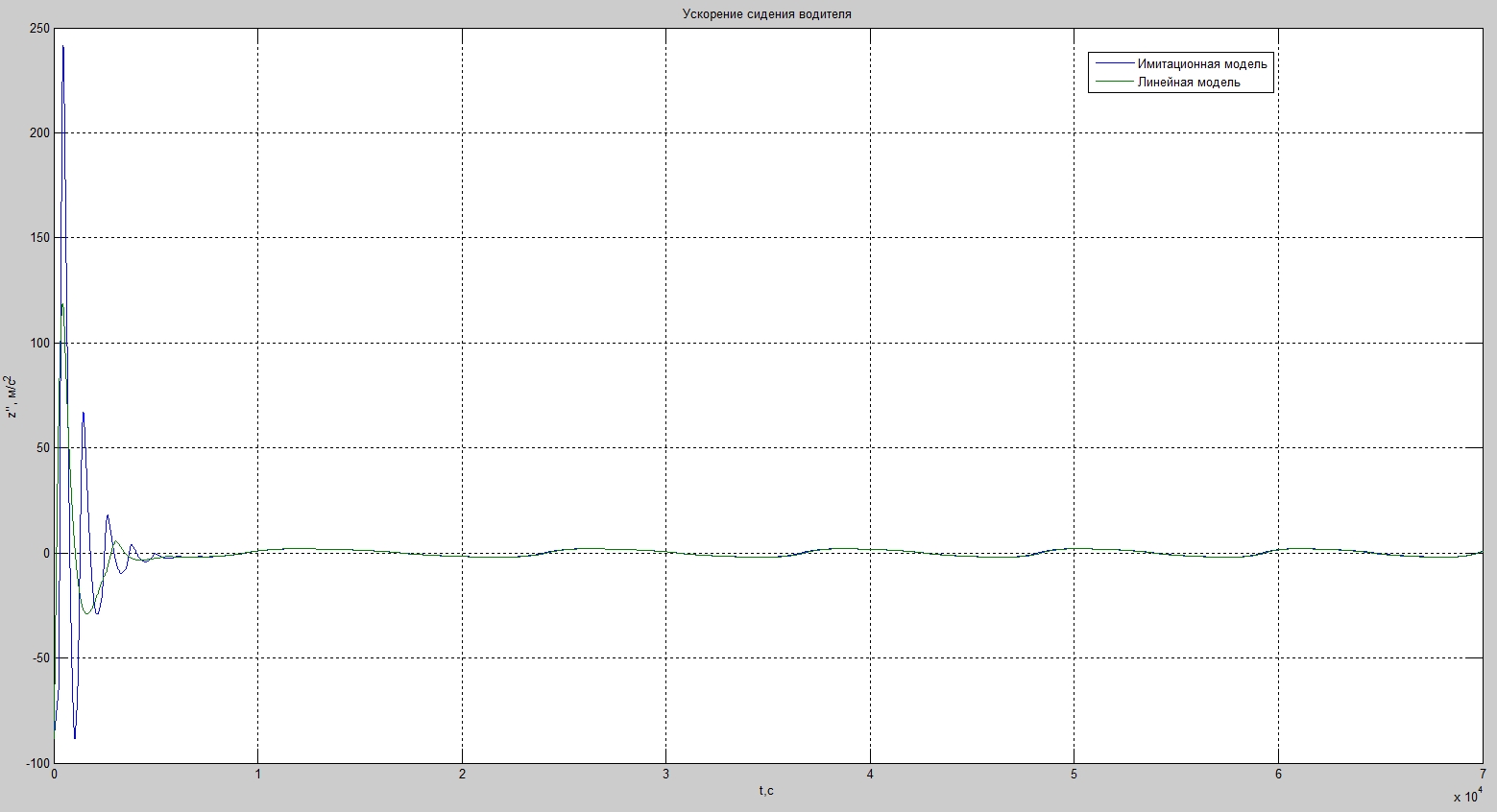
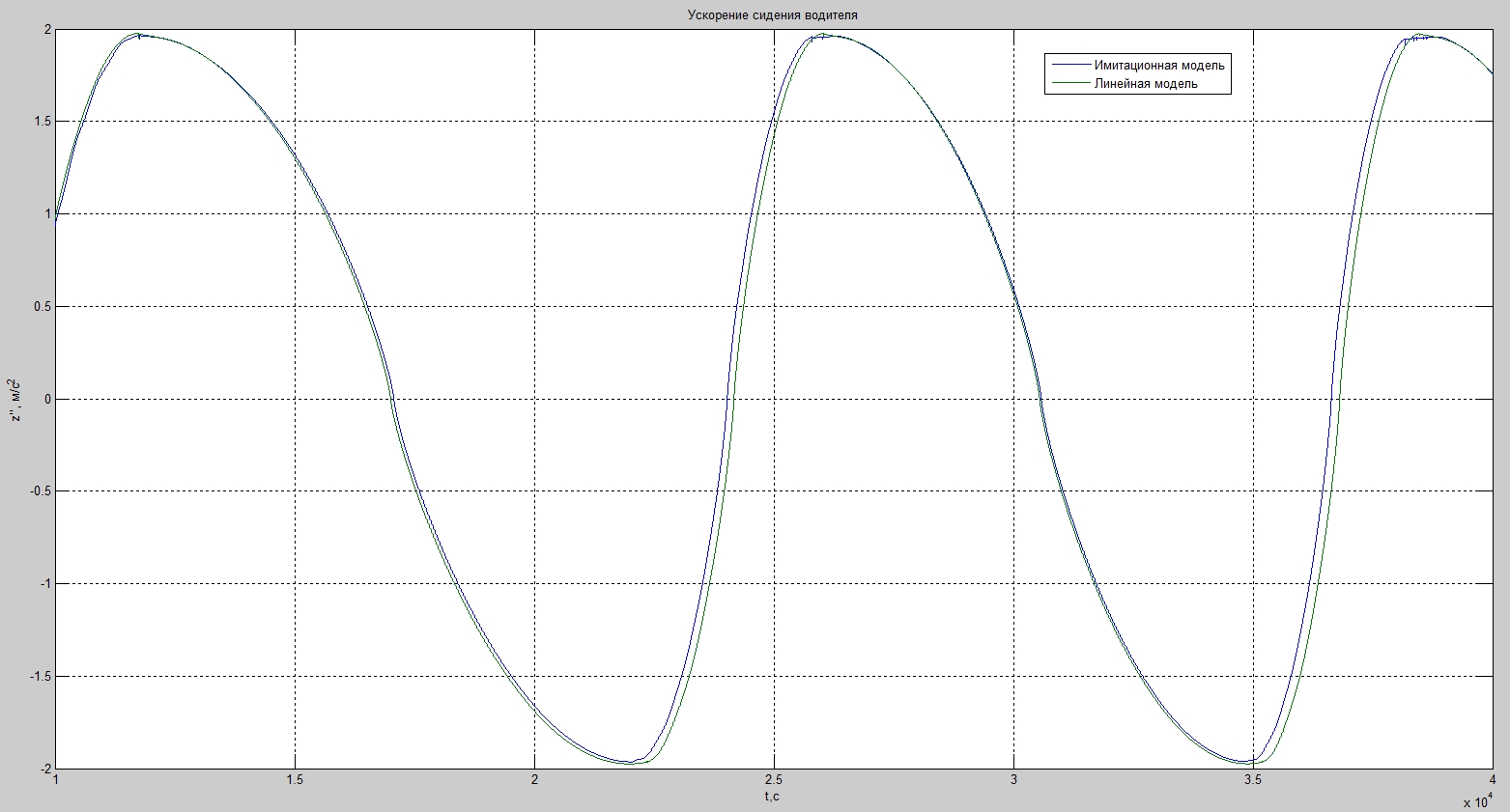
При коэффициенте упругости, полученном с помощью имитационной модели:
В качестве критерия плавности хода будем использовать величину ускорения на водительском месте.
Неустановившийся процесс, протекающий до 1 секунды, отбрасываем и рассматриваем полученный результат.
На представленных рисунках наложены два графика, полученные при постоянном коэффициенте жёсткости и с помощью имитационной модели. Как видно получившиеся зависимости ускорения от времени несколько различаются.
Список использованных источников
- Шеннон Р. Имитационное моделирование систем – искусство и наука. - М.: Мир, 1978, с.212.
- Help программы MatLab.
- Жеглов Л.Ф. Спектральный метод расчета систем подрессоривания колесных машин: учеб. Пособие / Л.Ф. Жеглов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. – 150с: ил.
- Пневмогидравлические рессоры подвесок автотранспортных средств: Монография/В.В. Новиков, И.М. Рябов; Волгоград. гос. техн. ун-т. – Волгоград, 2004. – 311с.